Proportional aggregation of preferences for sequential decision making

Problem Statement

In various decision-making contexts, such as recommendation systems or hiring processes, groups often make a series of decisions. A common but naive approach is to select the option with the most supporters in each round. However, this can result in unrepresentative outcomes where the majority dominates all decisions, potentially discouraging participation from minority groups.

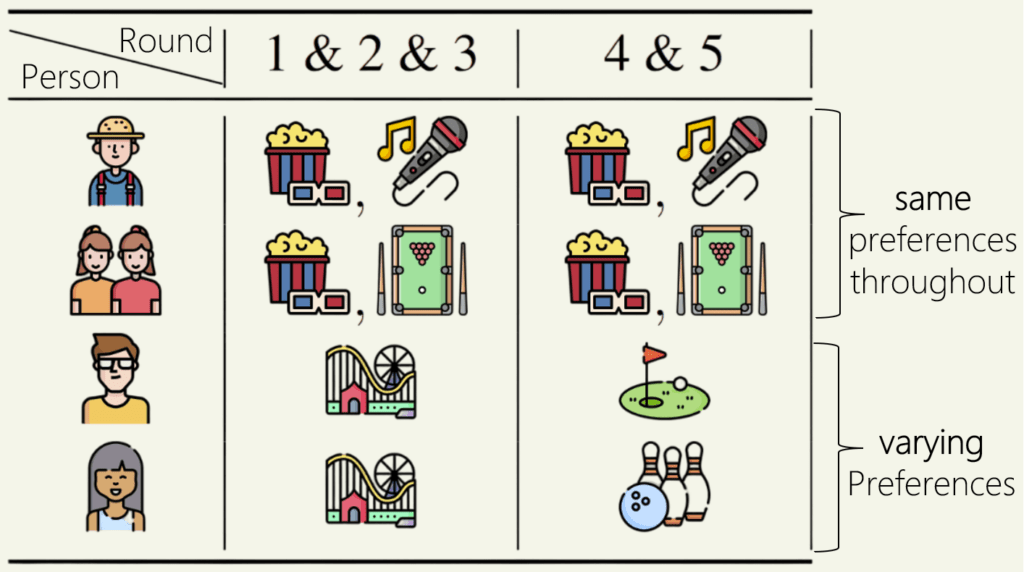
Consider a scenario where a group of friends (voters) want to hang out weekly. They have different preferences for activities (alternatives) each week (round), but only one activity can be chosen. This means the entire group ends up doing one activity, even if some members dislike it.

In the example above, five friends have different preferences for activities each week. For instance, person 4 prefers amusement parks for the first three rounds and golf for the last two. Movies are the majority choice every week, supported by persons 1-3, which is of the group. However, consistently choosing movies would leave persons 4 and 5 unsatisfied.

Can we find a more equitable solution that fairly represents everyone’s preferences? This paper addresses this challenge for sequential decision-making problems using approval votes, through the lens of Social Choice Theory.

Applications

Let’s explore some applications where this problem arises:

• Hiring Processes (University): Departments need to hire new faculty members. Existing faculty want to recruit collaborators. How can we ensure that the department’s diverse research interests are represented over multiple hiring rounds?
• Virtual Democracy: When making repeated decisions, machine learning can model user preferences, which can be used when eliciting preferences is costly. For example, AI systems making ethical decisions quickly, such as autonomous vehicles in moral dilemmas, should fairly reflect people’s preferences.
• Uncertainty about the Goal: Managing an intelligent system (like a robot) that repeatedly decides on actions to maximize an objective function can be challenging if the desired objective function is uncertain. We might decide on a mixture of objectives (e.g., 20% on objective 1). Over multiple decisions, the system should ensure each objective is satisfied proportionally to its importance.

Main Idea: Proportionality Axioms

The core fairness concept we study is proportionality. Hypothetically, if a group makes decisions over 10 rounds and 30% always prefer movies while 70% always prefer golf, then 3 out of 10 decisions should be movies, and 7 out of 10 should be golf. While a single decision might favor the majority, over multiple rounds, we can aim to satisfy different groups in each round for more equitable outcomes.

However, real-world scenarios don’t always have well-defined ‘groups,’ and the set of alternatives might change each round, forming new groups. Voters who agree once might disagree later. How do we incorporate such variations?

We say a « group » (of voters) agrees in a round if one or more alternatives are approved by all of them.

We propose proportionality guarantees of the following form: Every group of % voters that agrees in of the rounds, must approve % of the decisions:

But what does it mean for a group to approve % of decisions?

We can’t have all members of the group approving % of the decisions. Prior work has shown that this property can’t be satisfied in even simpler settings like apportionment (where the alternatives and approval profile of every voter are the same in each round) — (Example 1).

So we study two types of (weaker) guarantees based on individual members of that can actually be satisfied (as we will show later).

Strong Proportional Justified Representation (Strong-PJR): There are at least % rounds where any member of approves the decision of that round.

Strong Extended Justified Representation (Strong-EJR): There is at least one consistent member of that approves the decision of % rounds.

If satisfies Strong-EJR, then the % rounds where the lucky member of approves decisions help satisfy Strong-PJR. Thus, satisfying Strong-EJR implies satisfying Strong-PJR.

Let’s understand these axioms with the friends’ outings example presented earlier.

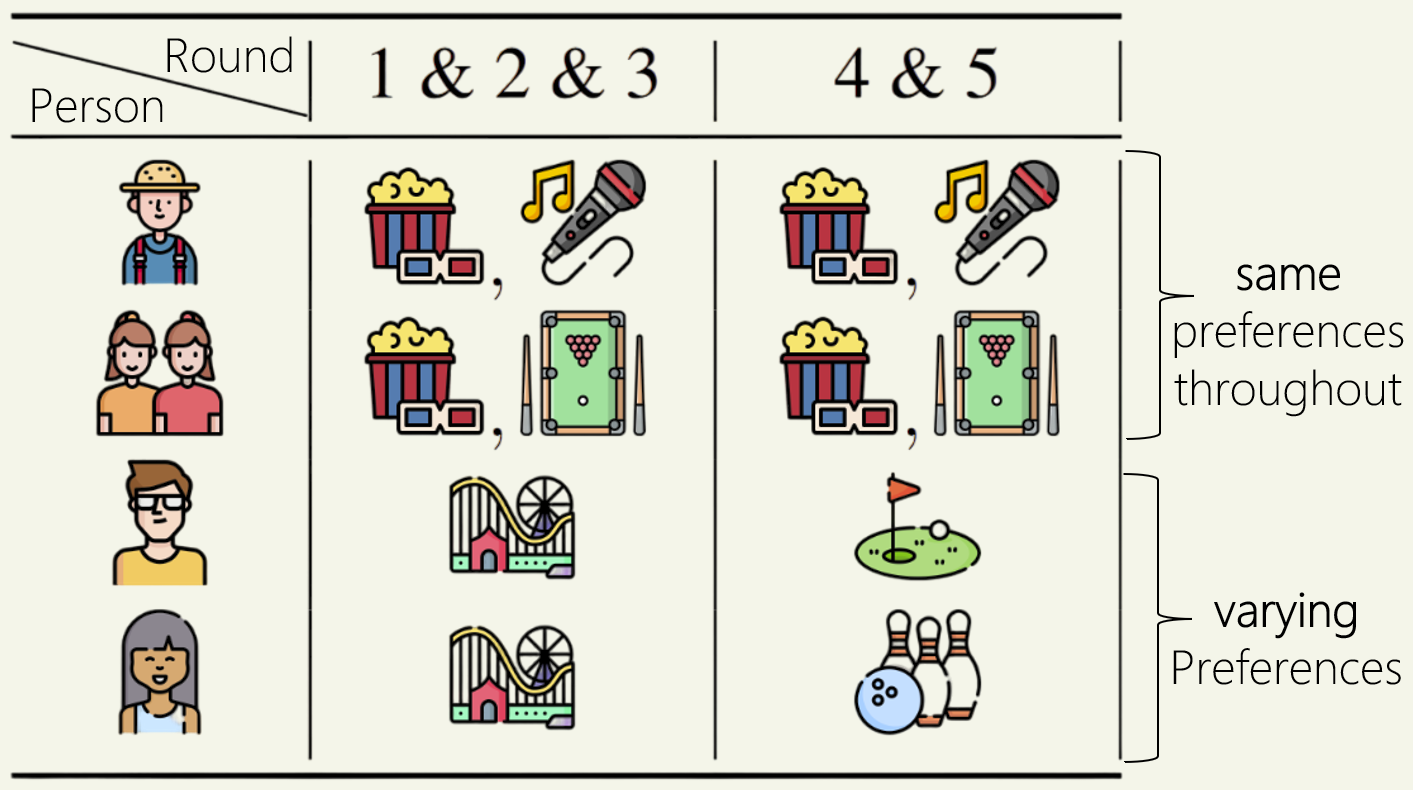
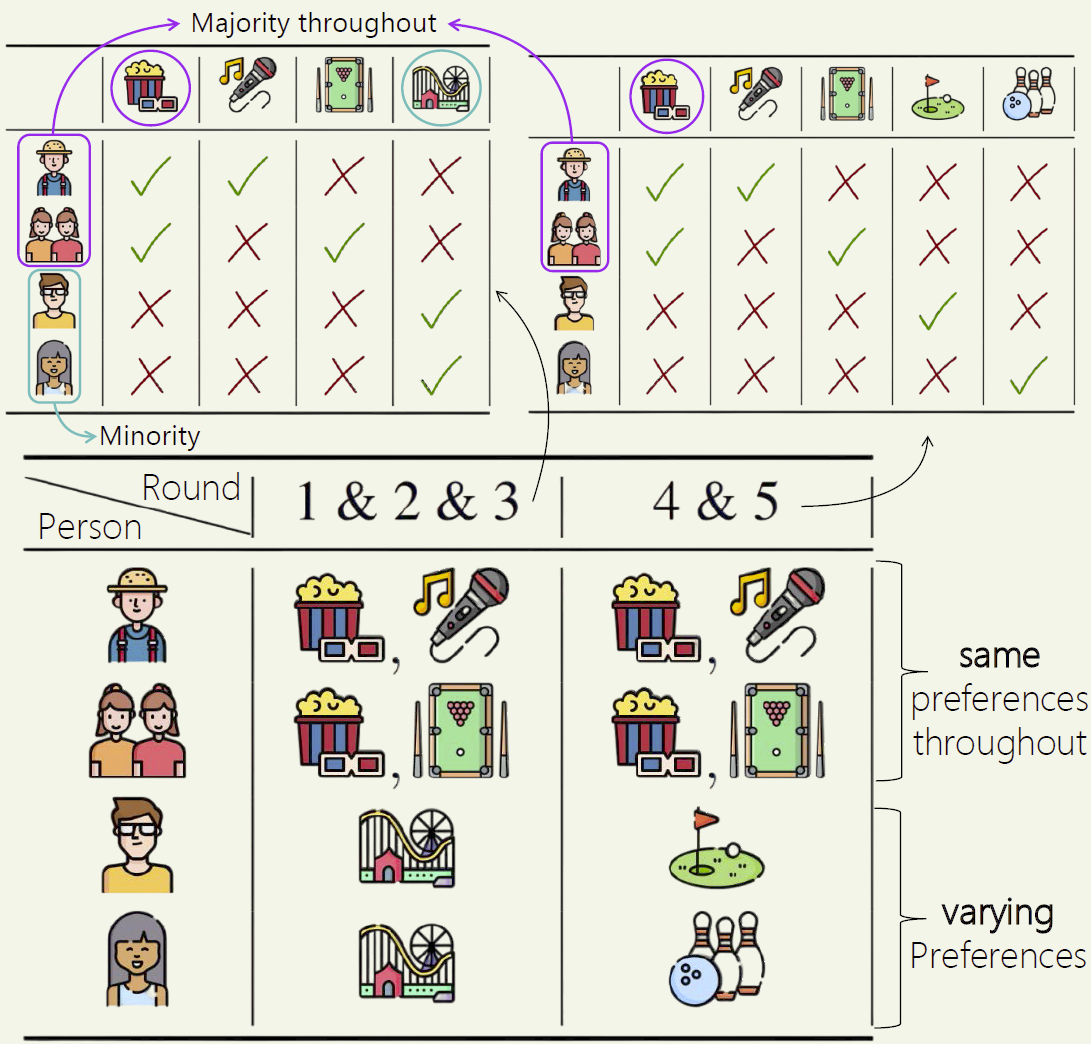
Let Group A be persons 1-3 (the group with the same preferences in the picture above), and Group B be persons 4-5 (the rest of the people with varying preferences). First, how many decisions do these groups deserve?

Group A is 60% of voters, and they agree in every round through the movie alternative. Thus, they deserve to approve decisions of % rounds. Group B is 40% of voters, and they only agree in rounds 1-3 through the amusement park alternative. Thus, they deserve to approve decisions of % rounds.

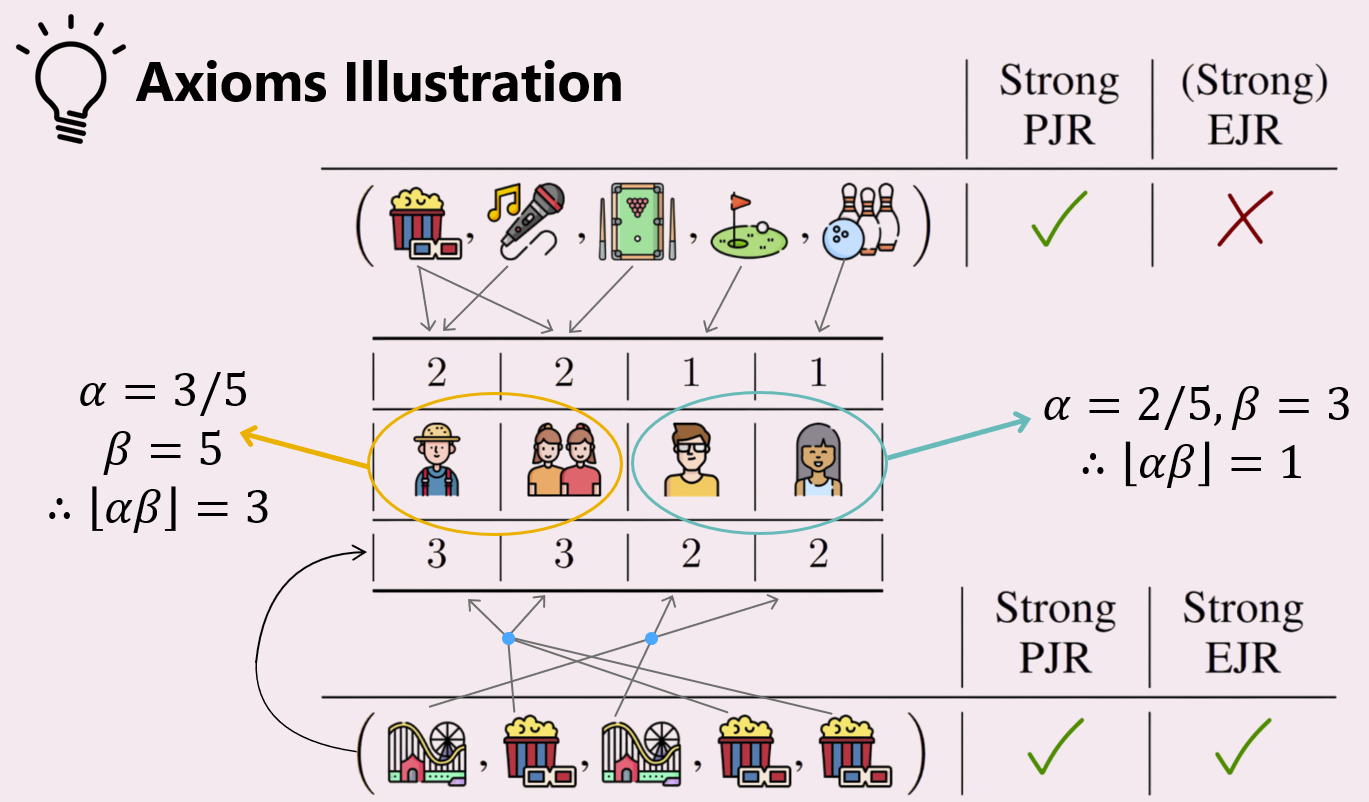
Now let’s consider the decision sequence on the top (of the above image), i.e., (movie, karaoke, pool, golf, bowling). Person 1 approves 2 decisions (rounds 1, 2), persons 2-3 approve 2 decisions (rounds 1, 3), and persons 4, 5 each approve 1 decision (rounds 4, 5 respectively).

For Strong-PJR, we need 3 rounds where any member of Group A approves the decision, and similarly 2 such rounds for Group B. We achieve this through rounds 1-3 for Group A, and rounds 4-5 for Group B. Thus, this sequence of decisions satisfies Strong-PJR.

However, for Strong-EJR, we

Source