Artificial Intelligence (AI) is now an integral part of our daily lives, influencing decisions from loan approvals to medical diagnoses. AI models use intelligent algorithms and data to make increasingly significant decisions. However, if we cannot understand these decisions, how can we trust them?
One way to make AI decisions more comprehensible is by using models that are inherently interpretable. These models are designed so that users can deduce the model’s behavior by examining its parameters. Popular inherently interpretable models include Decision Trees and Linear Regression. Our research, published at IJCAI 2024, introduces an enhancement to a broad class of such models, called logistic models, through a method known as Linearized Additive Models (LAM).
Our findings indicate that LAMs not only make the decisions of logistic models more understandable but also maintain high performance levels. This translates to better and more transparent AI for everyone.
To grasp LAMs and logistic models, consider the following scenario. Imagine you are a real estate agent trying to predict the price of a house based on its size. You have data on numerous houses1, including their sizes and prices. If you plot this data on a graph, linear regression helps you draw a straight line that best fits these points. This line can then be used to predict the price of a new house based on its size.
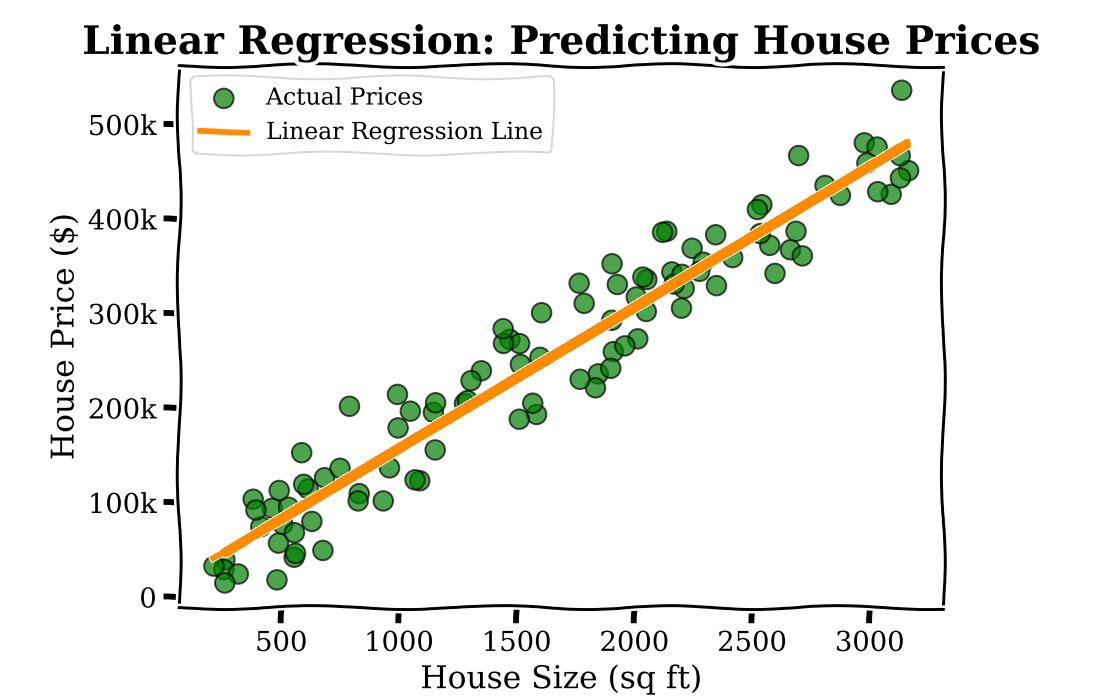
Linear regression is an inherently interpretable model, as the model’s parameters (here, a parameter associated with square footage, 
) have a straightforward interpretation: each additional square foot in house size incurs an additional cost of 
.
Now, imagine you are trying to predict something slightly different using the same data; namely, the binary outcome or yes-no question of whether a house’s price exceeds 
or not. Typically, a modeler here would use Logistic Regression. This method allows you to draw a curve that separates houses selling above this amount from those that do not, providing a probability for each house. In the graph below, we show a logistic regression to predict the sales status, whether the house sells for more than 
or not.
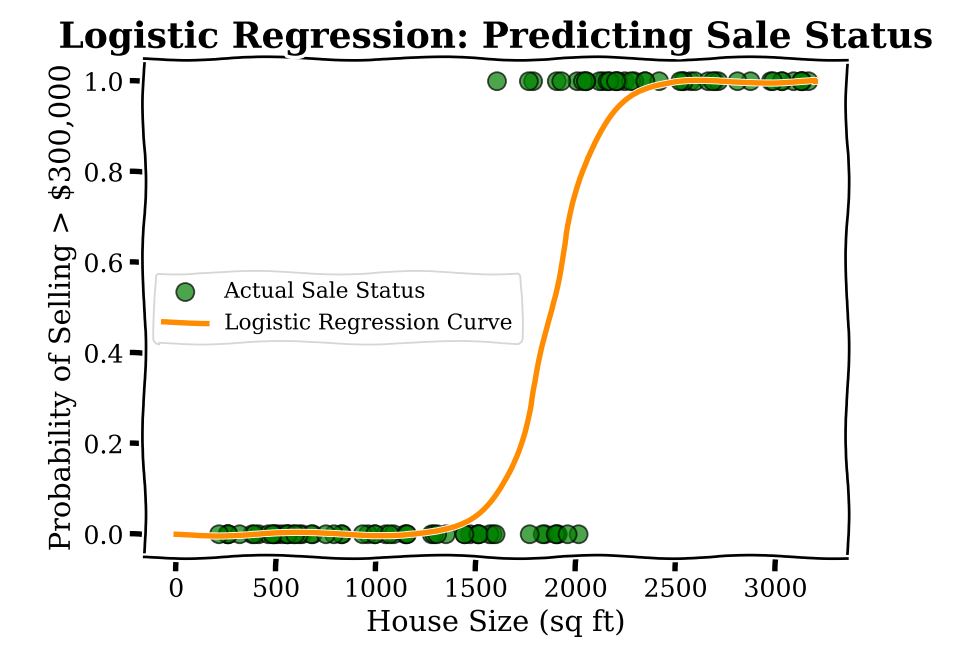
Unfortunately, while the model is transparent in that it does not have many parameters (for our example here, there are only two), logistic regression coefficients do not have a simple interpretation. For a given area, the additional cost incurred by adding 100 square feet is different. For instance, the probability change from 600 to 800 square feet is different from the probability change from 1,600 to 1,800 square feet. This is because, in a logistic regression model, the predicted probability of a sale is a non-linear function of square footage.
LAMs bring the interpretability of linear regression to models that predict yes-no responses, like logistic regression. We modify logistic models to use linear functions to predict probability. The method is straightforward and illustrated by the curve below.
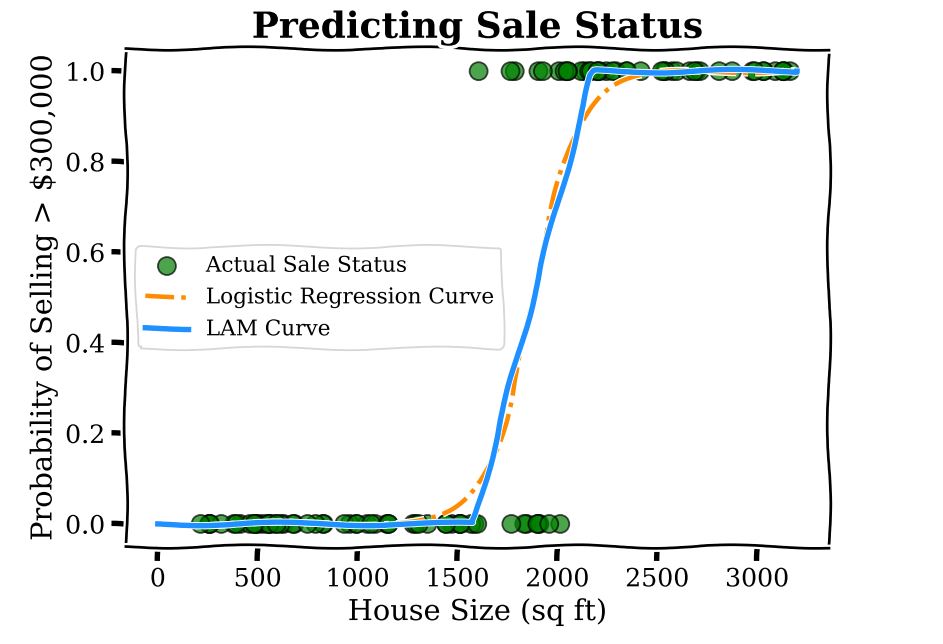
We have three regions: below 1,500 square feet, where the predicted probability of the price being above is zero; above 2,000 square feet where the probability is one; and the middle region of 1,500 to 2,000 square feet which linearly interpolates between the two regions, meaning the model’s output is obtained by drawing a straight line between the end of the zero-probability region and the start of the one-probability region. In this region, the coefficient corresponding to square footage is 
0.002, which is interpreted as each additional square foot increasing the predicted probability of sale by 0.002. As a concrete example, increasing the house size from 1,600 to 1,700 square feet increases the predicted sale probability by LAM by 0.2. This interpretation of the coefficient is the same if one increases the house size from 1,700 to 1,800 square feet, due to the linear function used.
Compare this with the logistic model for which we could not provide such a simple description of the model. Note that the LAM curve is very close to the logistic regression curve, which is intentional. LAMs leverage the efficient training routines developed over decades for logistic regression models and act as a post-processing step to enhance interpretability.
To understand which type of AI model is easier to use, we conducted a survey comparing traditional logistic models with our new Linearized Additive Models (LAM). Participants were presented with several scenarios where they had to predict how model outcomes would change based on different inputs.
In the first task, they guessed whether the output would increase or decrease. In the second task, they estimated the magnitude of the change. Finally, they told us which model they found easiest to use. We can observe the results in the graphs below.
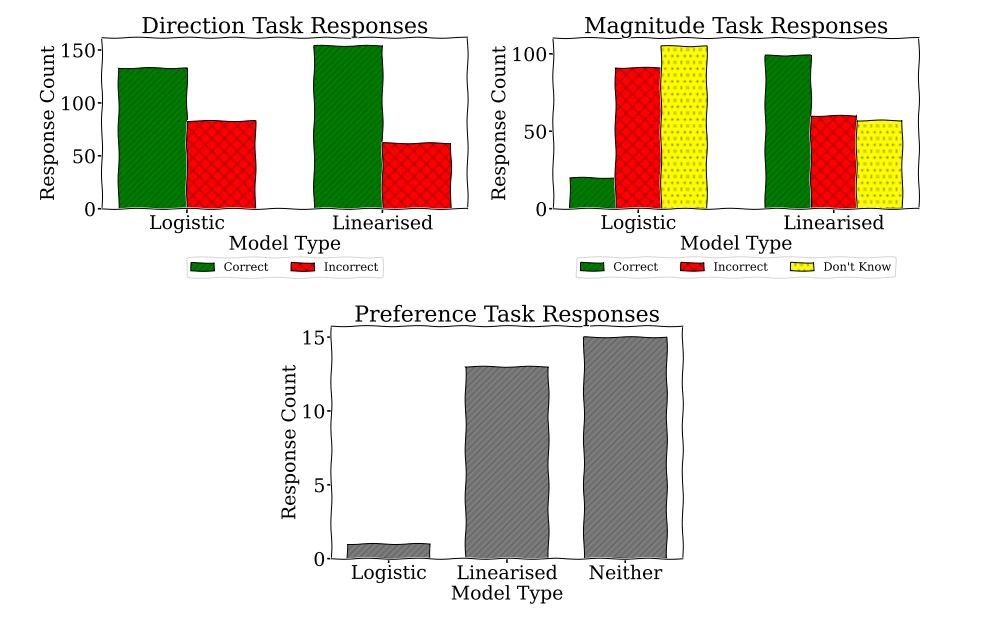
We found that people performed better in predicting the direction of change with LAMs. They were much better at estimating the magnitude of change with LAMs. Most participants reported that neither model was particularly easy to use, but more people preferred LAMs.
This suggests that LAMs are generally easier to understand and use, which could make AI decisions more transparent and reliable. However, the fact that many participants still find both models challenging indicates that we need better ways to help people understand how AI models work under the hood, especially when used for important decisions.
If you want to learn more about this work, you can read the full paper Are Logistic Models Really Interpretable?, Danial Dervovic, Freddy Lécué, Nicolás Marchesotti, Daniele Magazzeni.
1These data are synthetic, generated for this article.
Disclaimer: This blog post has been prepared for informational purposes by the Artificial Intelligence Research group of JPMorgan Chase & Co. and its affiliates (« JP Morgan ») and is not a product of JP Morgan’s Research Department. JP Morgan makes no representation or warranty whatsoever and disclaims all liability for the completeness, accuracy, or reliability of the information contained herein. This document is not intended to constitute investment research or investment advice, nor a recommendation, offer, or solicitation for the purchase or sale of any security, financial instrument, financial product, or service, or to be used in any way for evaluating the merits of participating in any transaction, and does not constitute a solicitation in any jurisdiction or to any person if such solicitation would be unlawful under the laws of such jurisdiction.
© 2024 JPMorgan Chase & Co. All rights reserved
