An example of a mission with a cycle and path maximizing the number of patients helped.
In their paper The Parameterized Complexity of Kidney Exchange Revisited presented at IJCAI 2024, Ursula Hébert-Johnson, Daniel Lokshtanov, Chinmay Sonar, and Vaishali Suryanarayana explore the kidney exchange problem. Ursula, Chinmay, and Vaishali discuss kidney exchange and how they have addressed two open problems in this field.
What is the topic of your paper and why is it such a vital area of study?
Kidney diseases affect tens of thousands of patients in the United States and hundreds of millions worldwide. One way to treat kidney failure is through regular dialysis. However, attending frequent appointments over the years is challenging, especially for the elderly. Another treatment option is obtaining a kidney transplant by joining a waiting list to be matched with a compatible donor. Unfortunately, the demand for kidney donations far exceeds the available transplants. Currently, the median wait time for a kidney transplant (from a deceased donor) is 4.05 years in the U.S., and many patients never find a compatible donor.
Patients often have a friend or family member willing to donate a kidney; however, the donor’s kidney type might not be compatible. In 2000, Kidney Paired Donation (KPD) was introduced to solve this issue and increase the number of patients receiving transplants. KPD is a centrally managed barter market for kidney donations. A patient with an incompatible donor can participate in the market hoping to exchange their donor with a compatible donor from another participating pair. The popularity of KPD has grown over the years, and it now operates in several countries, including the U.S., the U.K., the Netherlands, and India. KPD leads to a natural optimization problem known as the kidney exchange problem, where the goal is to maximize the number of patients receiving a transplant. In our paper, we present two algorithms that efficiently solve this problem and study its computational complexity.
Could you give us an overview of the kidney exchange problem: how does the method generally work?
To understand the kidney exchange problem, consider a compatibility graph where each node is either a patient-donor pair or a single donor (to allow for altruistic donors), and the edges between nodes denote compatibility, i.e., a directed edge from node X pointing to node Y indicates that the patient at node Y can receive a kidney from the donor at node X. A cycle in this graph provides a possible way to perform kidney exchanges where the patient at each node in the cycle gets a compatible kidney from the donor of the previous node. The other option is to find a path from an altruistic donor: in this case, each donor donates their kidney to the next pair on the path. The way to help the maximum number of patients is to find a set of non-overlapping cycles and paths that together include the maximum number of patients.
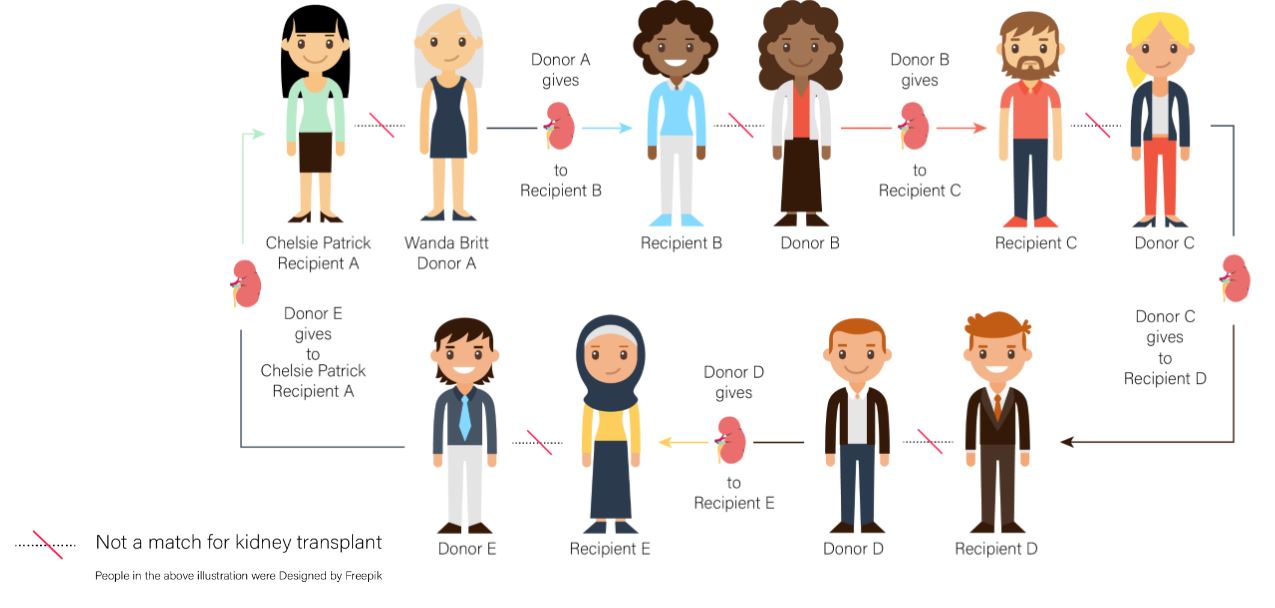An example of a kidney exchange cycle. Image credit: UNC School of Medicine.
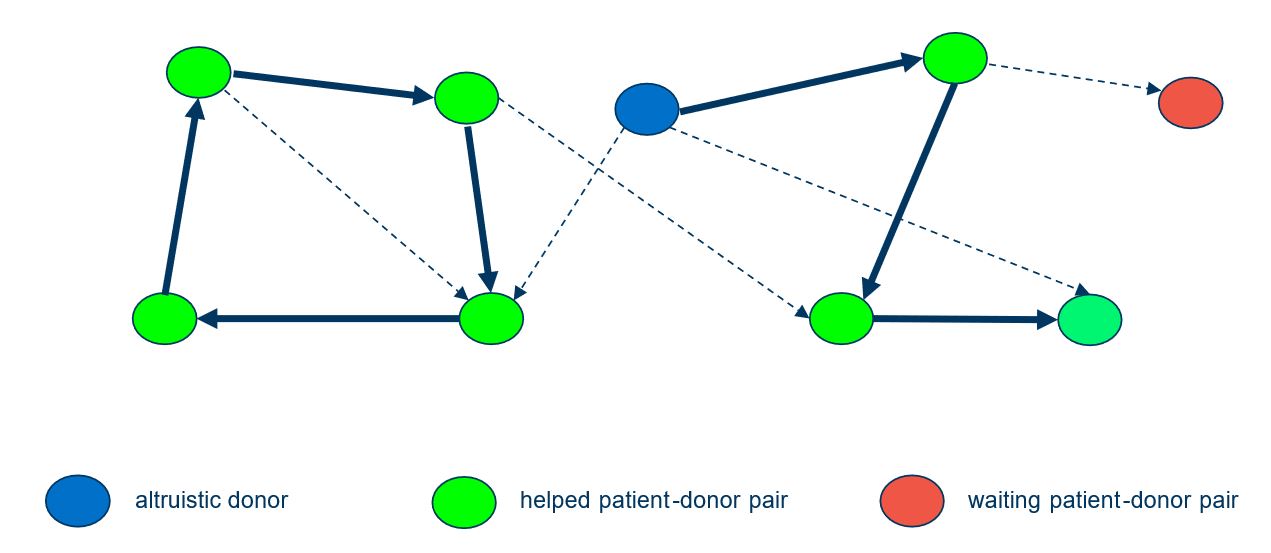An example of a mission with a cycle and path maximizing the number of patients helped.
Since KPD is a barter system, transplants for all patients in a cycle or path must be performed simultaneously; otherwise, a donor is not obligated to donate their kidney if the paired patient has already received one. This constraint requires us to choose relatively small cycles and paths in the final assignment.
KPD is overseen by health organizations in each participating country. For example, for the National Kidney Registry in the U.S., UCSF Health and UCLA Health offer a kidney exchange program. As the number of patients/donors increases, finding donor assignments to patients becomes computationally challenging (i.e., it can take a long time to find an optimal set of cycles and paths). To overcome this problem, researchers have mainly tried two different directions: one is to find an approximately optimal assignment (i.e., an assignment that does not help as many patients as the optimal but can be computed quickly), and the other approach is to understand structural properties of the compatibility graph to design efficient algorithms in certain cases. We adopt the second approach.
What are the main contributions of your paper?
The algorithms in our paper are parameterized algorithms, meaning that the running times are fast when certain parameters are small. Since the kidney exchange problem is NP-hard (meaning it is unlikely that there is an efficient polynomial-time algorithm that works in all cases), this problem is an excellent candidate for parameterized algorithms.
We present two algorithms in our paper, with the first being quite simple to state. For this one, the parameter is the number of patients receiving a kidney donation, so this algorithm can be used when the number of patients we hope to help is relatively small. For this case, we designed an efficient algorithm that, given t, either finds donors for at least t patients or determines that no such solution exists. The running time is about 4t, meaning this algorithm runs quickly when t is small, even though the running time is exponential in general.
For our second algorithm, we assume that the number of « kidney types » is relatively small. To see what this means, imagine two kidney donors (or patients), Kirk and Kendra, have the same blood type, age, and other medical characteristics. If all their relevant characteristics are the same, then the set of patients (or donors) with which Kirk and Kendra are compatible will be the same. This means Kirk and Kendra have the same « kidney type. » Our second algorithm works efficiently when the number of distinct kidney types is small. The running time is a doubly exponential function of the number of kidney types, so in a sense, it is slower than the first algorithm. The advantage of this approach, however, is that the number of kidney types is likely small in the real world. The number of patients we wish to help will often be large, but the number of blood groups, etc., can indeed be a small constant.
Looking at the open problems (from previous work) you have solved, could you talk a bit about your methodology? How did you go about solving these problems?
Before our paper, there was already a known algorithm for handling the kidney exchange problem (FPT), in the case where the parameter is the number of patients t receiving a kidney. The running time of this algorithm was about 161t, so our 4t algorithm significantly improves this. To say a bit more about our methods, our algorithm uses algebraic techniques. We expressed each possible solution as a term in a polynomial and used the properties of an associated group ring to check if a solution exists.
For the case where the parameter is the number of kidney types, we solved the open problem of whether there is an FPT algorithm for the kidney exchange problem in this scenario. For this algorithm, we formulated the problem as an integer linear program (ILP) that can be solved in FPT time, parameterized by the number of variables.
Are there any other open problems you would like to tackle next?
A natural next step in our research is to improve the running times of our algorithms. Another promising avenue is to apply the structural insights from our parameterized algorithms to develop heuristics that perform well on real-world data.
Some previous algorithms have successfully bridged the gap between theory and practice and are currently used to power kidney exchange programs in the U.S. Notably, one of the researchers behind these algorithms received the 2023 AAAI Award for AI for the Benefit of Humanity. Inspired by this, we are motivated to advance research in this important field.
This research was also presented by Vaishali during the UCSB Grad Slam finals, where students present a 3-minute pitch on their work. You can watch the recording below:
About the Authors
 | Úrsula Hébert-Johnson is a Ph.D. student in the Computer Science Department at UC Santa Barbara, advised by Daniel Lokshtanov. Her research focuses on parameterized graph algorithms and polynomial-time graph counting and sampling algorithms. She is particularly interested in graph algorithms that use algebraic techniques, such as the polynomial ring that can be used to describe solutions to the kidney exchange problem. Before joining UCSB, she earned her bachelor’s degree in mathematics from Stanford University. |
 | Chinmay Sonar is a machine learning scientist at Visa. His work focuses on developing generative AI models for video question answering tasks and real-time payment fraud detection systems (RTP). His recent research has been published in EMNLP, IJCAI, and ESA. Previously, he also worked on resource allocation problems in the broader AI domain, including kidney paired donation, facility location/clustering, and multi-winner elections. He recently completed his Ph.D. in computer science at the University of California, Santa Barbara. He also holds a bachelor’s and master’s degree from the Indian Institute of Technology (IIT) Gandhinagar. |
 | Vaishali Surianarayanan is a senior Ph.D. student at the CS Theory Lab at UC Santa Barbara. Her research focuses on using parameterization for algorithm design, both in theory and practice, for graph problems arising from various domains. She is also interested in databases and distributed systems and has interned in research and industry in this area. Her work has been published in leading AI and CS theory conferences such as FOCS, SODA, and IJCAI. Outside of research, she enjoys teaching and actively advocates for diversity, equity, and inclusion in technology. In her free time, she is often found with her sketchbook. |
Lucy Smith, Editor-in-Chief of AIhub.
